Sep 02, 2020
Drawing with DFT and Epicycles
Draw any figure using maths with the use of DFT(fouries series in exponential form) and epicycle
Example
| real figure |
|---|
|
| generated figure |
|---|
|
Installation
Install ffmpeg You will need to install ffmpeg to write the animation to video file
$ sudo apt-get update
$ sudo apt-get install ffmpeg
Clone the repository
$ git clone https://github.com/Amritaryal44/drawing-with-DFT-and-epicycle.git
Install all package requirements for python
$ pip install -r requirements.txt
DFT_epicycle explaination
1. Read the image and convert to gray scale
img = cv2.imread("nepal.png")
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
2. Threshold the gray image to get pure black and white image
ret, thresh = cv2.threshold(img_gray, 127, 255, 0)
3. Find the contour of image
contours, hierarchy = cv2.findContours(thresh, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)
We get two contours here:
contours[0] |
|---|
|
contours[1] |
|---|
|
But we need contours[1]. so:
contours = np.array(contours[1])
4. Split the points and store in x_list and y_list
Without reshaping:
x_list, y_list = contours[:, :, 0], -contours[:, :, 1]
print(x_list.shape)
Note that
y_listis given as-contours[:, :, 1]because we want the y points to be upright.
Output:
(5541, 1)
So the shape is in 2D. To make it 1D:
We are making it in 1D because later we will need 1D data for making f(t) in
np.interp()function
x_list, y_list = contours[:, :, 0].reshape(-1,), -contours[:, :, 1].reshape(-1,)
print(x_list.shape)
Note that for reshaping (a,b), (-1,) is similar to (a*b,)
Output:
(5541,)
If you plot the points in matplotlib, you will get:
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x_list, y_list)
plt.show()
output:
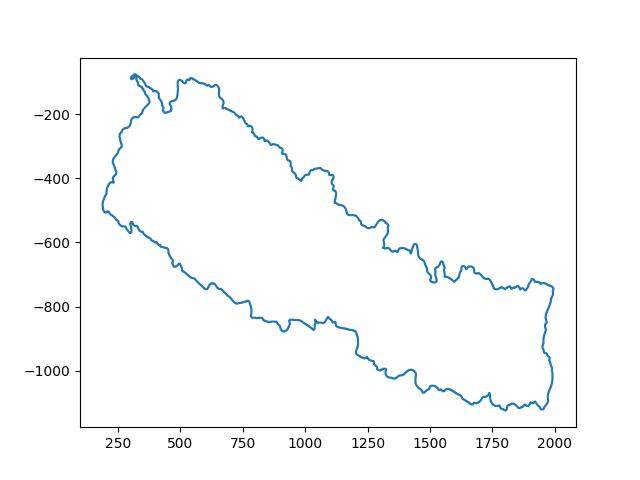
(1000, -600) But we want the figure to be centered at (0,0) for using fourier series calculation easily.
5. Centering the points to origin: (0,0)
# center the contour to origin
x_list = x_list - np.mean(x_list)
y_list = y_list - np.mean(y_list)
Here, we are translating every points by mean of points. We are doing just translation operation here. If you plot the points in matplotlib again, you will get:
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x_list, y_list)
plt.show()
output:
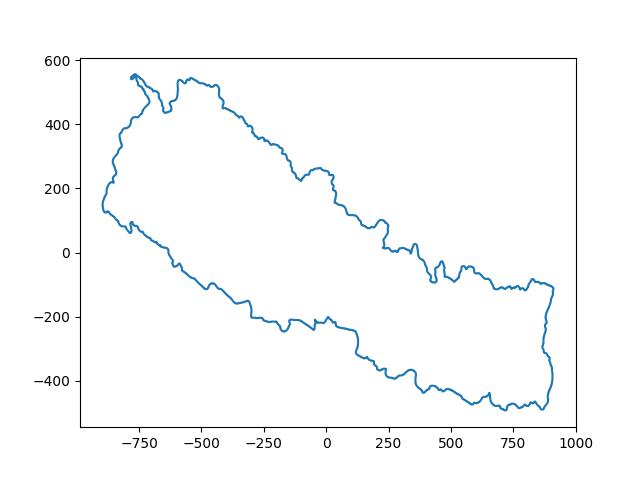
Store the size information of the figure because later you will want the generated image to be fit in the figure. We will use it later.
xlim_data = plt.xlim()
ylim_data = plt.ylim()
6. Make a time_list from 0 to
We are doing this, because we are rotating the circle. To rotate a circle, we need angle. Later we will use this angle to determine
t_list = np.linspace(0, tau, len(x_list))
print(t_list)
Output:
[0.00000000e+00 1.13414897e-03 2.26829794e-03 ... 6.28091701e+00
6.28205116e+00 6.28318531e+00]
It will go from 0 to tau. Tau is just equal to
7. Find the fourier coefficients to approximately locate given points
Fourier Coefficient Formula is:
where :
coefficient calculated which is in form or where r is radius of circle and t gives the position of point in circumference of circle.
returns x, y points at time t. Note that we have created time_list. that was for this. t = time i.e from 0 to
Please watch this video for better understanding.
Coefficients will be in sequence like: …
More and more coefficients means better result.
So we will define order=100 for now. which goes from
order = 100
Let us make a loop to store coefficients in c
c = [] # a list to store coefficients from -order to order
for n in range(-order, order+1):
pass
Now this loop will go from -order to order.
Let’s make a function
def f(t, t_list, x_list, y_list):
return np.interp(t, t_list, x_list + 1j*y_list)
Here, np.interp() is used to generate x+iy at time t.
Let me clear you a bit.
x = 2
xp = [1, 3, 5]
yp = [10+20j, 30+40j, 50+60j]
y = np.interp(x, xp, yp)
print (y)
output:
(20+30j)
You see it was that simple. Now Let’s go to the loop and use the fourier coefficient formula.
c = [] # a list to store coefficients from -order to order
for n in range(-order, order+1):
coef = 1/tau*quad_vec(lambda t: f(t, t_list, x_list, y_list)*np.exp(-n*t*1j), 0, tau, limit=100, full_output=1)[0]
c.append(coef)
scipy.integrate.quad_vec() is used to do defininte integration over complex data.
Here we put [0] at the end of quad_vec() because quad_vec() returns (value, error).
After integration, we will append the coefficient in list.
Let me demonstrate quad_vec() in simple way.
def f(x):
return x+1j
# using scipy.integrate.quad() method
result = quad_vec(lambda x: f(x), 0, 3)[0]
print(result)
The above code does the formula:
Try it yourself. You will get almost same output as below. output:
(4.5+3.000000000000001j)
Now we are done with finding coefficients.
Note that tqdm is used for making progressbar. I will not explain it.
If you want to save the coefficients for later use, you can save it.
# convert list into numpy array
c = np.array(c)
# save it
np.save("coeff.npy", c)
Hurray!!! We are almost done.
Now time to make animation.
This is the interesting part of this project. We will make about 300 rotating circles to draw the figure we wanted.
Let me show you how circles and coefficients are related
For example, we have 3 coefficients.
When we plot the coefficients in figure, we will get result as follow:
|
| adding |
|---|
|
| adding |
|---|
|
and |
The direction of last circle is used to plot the drawing points.
In this way, circles are created. But we have to sort the coefficients to get the order like:
1. Let’s make a function to sort the coefficients.
Our coefficient is arranged as:
# Let us assume the coefficients as given in example
coeffs = np.array([2-2j,10+5j,-10-10j])
order = 1
def sort_coeff(coeffs):
new_coeffs = []
new_coeffs.append(coeffs[order])
for i in range(1, order+1):
new_coeffs.extend([coeffs[order+i],coeffs[order-i]])
return np.array(new_coeffs)
print(sort_coeff(coeffs))
Output:
[ 10. +5.j -10.-10.j 2. -2.j]
Look at the output, we have sorted them in order like:
2. How to make circles and lines in matplotlib
Making a circle<br>
Formula for ploting the circle is :
fig, ax = plt.subplots()
ax.set_aspect('equal') # to make the axes symmetric
theta = np.linspace(0, tau, num=50) # 0, ...,... , tau
r = 20
x, y = r * np.cos(theta), r * np.sin(theta)
ax.plot(x, y, 'r-')
plt.show()
Output:
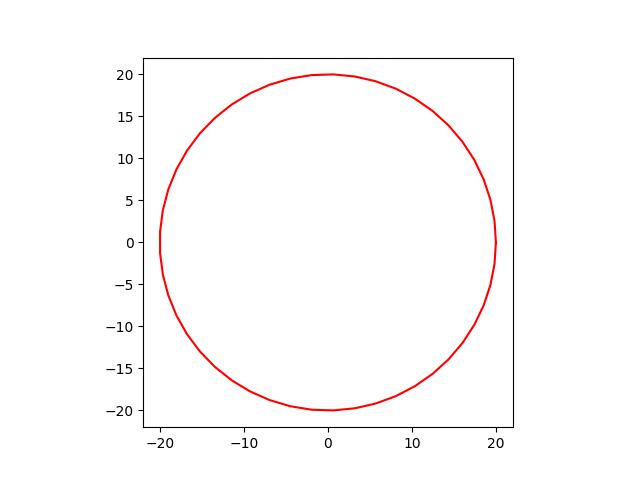
Making a radius in circle show direction of rotation<br>
Let us copy the circle code and make a line here.<br>
We will draw the line from center of circle and align at
fig, ax = plt.subplots()
ax.set_aspect('equal') # to make the axes symmetric
theta = np.linspace(0, tau, num=50) # 0, ...,... , tau
r = 20
x, y = r * np.cos(theta), r * np.sin(theta)
# draw a line to indicate the direction of circle
x, y = [0, r*np.cos(tau/8)], [0, r*np.sin(tau/8)]
ax.plot(x, y, 'g-')
ax.plot(x, y, 'r-')
plt.show()
I hope you understand how to make lines and circles in matplotlib. Later we will use the code directly.
3. Now we will join the circles and lines in the figure
Note that center point of next circle is the coefficient point of a circle.
I have already said that coefficients are nothing but information about the radius and radius direction in current circle. To rotate a circle, we can do:
Now let’s make the function.
def make_frame(i, time, coeffs):
pass
Here, time is list of angles from 0 to tau. this is responsible for animation.
i is the frame number. It will go from 0 to len(time).
Now inside the function, we will follow following steps.
I. First of all we need to break the coefficients into x_coefficient and y_coefficient.
code:
# sort the coefficient first.
coeffs = sort_coeff(coeffs)
# split into x and y coefficients
x_coeffs = np.real(coeffs)
y_coeffs = np.imag(coeffs)
II. Loop to make all the circles for all coefficients
code inside function:
# make all circles i.e epicycle
for i, (x_coeff, y_coeff) in enumerate(zip(x_coeffs, y_coeffs)):
# calculate radius of current circle
r = np.linalg.norm([x_coeff, y_coeff]) # similar to magnitude: sqrt(x^2+y^2)
theta = np.linspace(0, tau, num=50) # theta should go from 0 to 2*PI to get all points of circle
x, y = center_x + r * np.cos(theta), center_y + r * np.sin(theta)
circles[i].set_data(x, y)
You may be confused about the circles[i].set_data(x, y)
We need to define it first. Let’s go out of the function and define all necessary parameters.
# make figure for animation
fig, ax = plt.subplots()
# different plots to make epicycle
# there are -order to order numbers of circles
circles = [ax.plot([], [], 'r-')[0] for i in range(-order, order+1)]
# circle_lines are radius of each circles
circle_lines = [ax.plot([], [], 'b-')[0] for i in range(-order, order+1)]
# drawing is plot of final drawing
drawing, = ax.plot([], [], 'k-', linewidth=2)
# to fix the size of figure so that the figure does not get cropped/trimmed
ax.set_xlim(xlim_data[0]-200, xlim_data[1]+200)
ax.set_ylim(ylim_data[0]-200, ylim_data[1]+200)
# hide axes
ax.set_axis_off()
# to have symmetric axes
ax.set_aspect('equal')
Again let’s go inside the function and proceed the code. Now we will make the radius line.
# center points for fisrt circle
center_x, center_y = 0, 0
# make all circles i.e epicycle
for i, (x_coeff, y_coeff) in enumerate(zip(x_coeffs, y_coeffs)):
# calculate radius of current circle
r = np.linalg.norm([x_coeff, y_coeff]) # similar to magnitude: sqrt(x^2+y^2)
theta = np.linspace(0, tau, num=50) # theta should go from 0 to 2*PI to get all points of circle
x, y = center_x + r * np.cos(theta), center_y + r * np.sin(theta)
circles[i].set_data(x, y)
# draw a line to indicate the direction of circle
x, y = [center_x, center_x + x_coeff], [center_y, center_y + y_coeff]
circle_lines[i].set_data(x, y)
# calculate center for next circle
center_x, center_y = center_x + x_coeff, center_y + y_coeff
What is the damn i for??
How to make animation??
Remember!!!
We need to multiply coefficient with exponential term as discussed already.
So, let’s multiply the coefficients with exponential term before sorting out.
# exponential term to be multiplied with coefficient
exp_term = np.array([np.exp(n*t*1j) for n in range(-order, order+1)])
# sort the terms of fourier expression
coeffs = sort_coeff(coeffs*exp_term)
Code upto now should be like:
def make_frame(i, time, coeffs):
global pbar
# get t from time
t = time[i]
# exponential term to be multiplied with coefficient
# this is responsible for making rotation of circle
exp_term = np.array([np.exp(n*t*1j) for n in range(-order, order+1)])
# sort the terms of fourier expression
coeffs = sort_coeff(coeffs*exp_term) # coeffs*exp_term makes the circle rotate.
# coeffs itself gives only direction and size of circle
# split into x and y coefficients
x_coeffs = np.real(coeffs)
y_coeffs = np.imag(coeffs)
# center points for fisrt circle
center_x, center_y = 0, 0
# make all circles i.e epicycle
for i, (x_coeff, y_coeff) in enumerate(zip(x_coeffs, y_coeffs)):
# calculate radius of current circle
r = np.linalg.norm([x_coeff, y_coeff]) # similar to magnitude: sqrt(x^2+y^2)
# draw circle with given radius at given center points of circle
# circumference points: x = center_x + r * cos(theta), y = center_y + r * sin(theta)
theta = np.linspace(0, tau, num=50) # theta should go from 0 to 2*PI to get all points of circle
x, y = center_x + r * np.cos(theta), center_y + r * np.sin(theta)
circles[i].set_data(x, y)
# draw a line to indicate the direction of circle
x, y = [center_x, center_x + x_coeff], [center_y, center_y + y_coeff]
circle_lines[i].set_data(x, y)
# calculate center for next circle
center_x, center_y = center_x + x_coeff, center_y + y_coeff
Now we need to draw the figure. As I have already said that the last center point we get is the point of figure.
We need to save all the last points (center_x, center_y) in a list say draw_x and draw_y.
THe whole code of make_frame() should be:
draw_x, draw_y = [], []
def make_frame(i, time, coeffs):
global pbar
# get t from time
t = time[i]
# exponential term to be multiplied with coefficient
# this is responsible for making rotation of circle
exp_term = np.array([np.exp(n*t*1j) for n in range(-order, order+1)])
# sort the terms of fourier expression
coeffs = sort_coeff(coeffs*exp_term) # coeffs*exp_term makes the circle rotate.
# coeffs itself gives only direction and size of circle
# split into x and y coefficients
x_coeffs = np.real(coeffs)
y_coeffs = np.imag(coeffs)
# center points for fisrt circle
center_x, center_y = 0, 0
# make all circles i.e epicycle
for i, (x_coeff, y_coeff) in enumerate(zip(x_coeffs, y_coeffs)):
# calculate radius of current circle
r = np.linalg.norm([x_coeff, y_coeff]) # similar to magnitude: sqrt(x^2+y^2)
# draw circle with given radius at given center points of circle
# circumference points: x = center_x + r * cos(theta), y = center_y + r * sin(theta)
theta = np.linspace(0, tau, num=50) # theta should go from 0 to 2*PI to get all points of circle
x, y = center_x + r * np.cos(theta), center_y + r * np.sin(theta)
circles[i].set_data(x, y)
# draw a line to indicate the direction of circle
x, y = [center_x, center_x + x_coeff], [center_y, center_y + y_coeff]
circle_lines[i].set_data(x, y)
# calculate center for next circle
center_x, center_y = center_x + x_coeff, center_y + y_coeff
# center points now are points from last circle
# these points are used as drawing points
draw_x.append(center_x)
draw_y.append(center_y)
# draw the curve from last point
drawing.set_data(draw_x, draw_y)
4. Making animation with matplotlib
Take your time and understand this code. An example code:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
def update_line(num, data, line):
line.set_data(data[..., :num])
return line,
# Set up formatting for the movie files
Writer = animation.writers['ffmpeg']
writer = Writer(fps=15, metadata=dict(artist='Me'), bitrate=1800)
fig1 = plt.figure()
data = np.random.rand(2, 25)
l, = plt.plot([], [], 'r-')
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.xlabel('x')
plt.title('test')
anim = animation.FuncAnimation(fig1, update_line, 25, fargs=(data, l),
interval=50)
anim.save('lines.mp4', writer=writer)
Now, we will use the same style of code for our code.
In place of update_line(), we will use make_frame() function.
The first parameter is i in make_frame() which will be frame number supplied over time.
Other parameters are placed in fargs=(time, c) as we need time and coefficients as argument.
Let’s say we want the total frames to be 300. Then we need to put frames=300 in animation.FuncAnimation() .
time should be from 0 to tau with 300 numbers.
So the code will be like:
# make animation
# time is array from 0 to tau
frames = 300
time = np.linspace(0, tau, num=frames)
anim = animation.FuncAnimation(fig, make_frame, frames=frames, fargs=(time, c),interval=5)
anim.save('epicycle.mp4', writer=writer)
pbar.close()
print("completed: epicycle.mp4")
Hurray!!! We are done.
I am very thankful to youtube/3Blue1Brown for their wonderful explanation.
Link to Git Repository: Drawing with DFT and epicycle

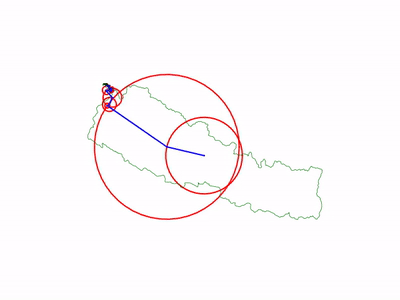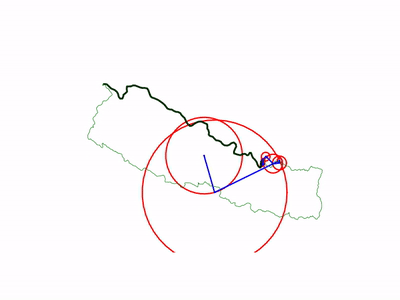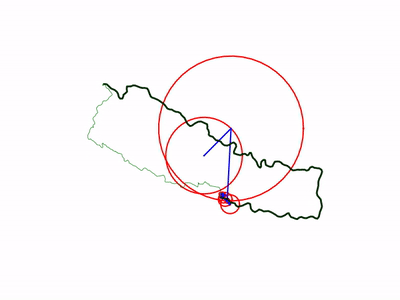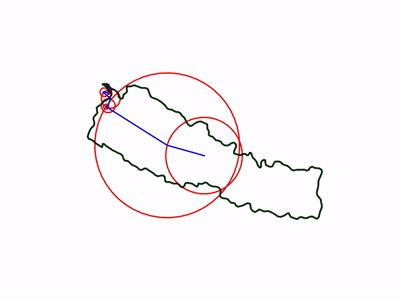

![coeff[0]](/posts/images/2/2-7.jpg)
![coeff[1]](/posts/images/2/2-8.jpg)
![coeff[-1]](/posts/images/2/2-9.jpg)